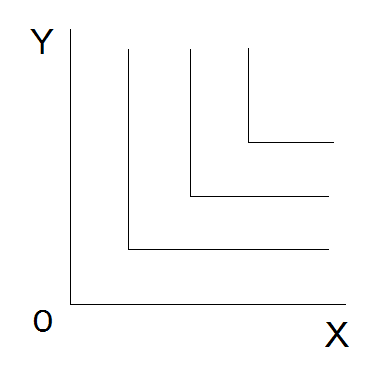レオンチェフ型関数

レオンチェフ型関数（れおんちぇふがたかんすう、英: The Leontief function）とは、投入要素が互いに完全補完で常に同じ比率の投入が行われる生産関数や効用関数のこと。ワシリー・レオンチェフに因んで名づけられた。

概要

レオンチェフ型生産関数では、生産要素が互いに完全補完（英: Perfect complement）で、要素需要量の比率が常に一定になる。レオンチェフ型効用関数では、財が互いに完全補完で、財への需要量の比率が常に一定になる。CES型関数の代替の弾力性をゼロに近づけた極限がレオンチェフ型関数となる。

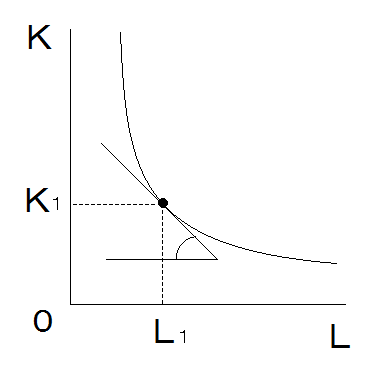
以下のような生産関数を考える。

${\displaystyle q={\text{min}}\left\{{\frac {z_{1}}{a}},{\frac {z_{2}}{b}}\right\}}$

ただしqは生産量、z₁は生産要素1の投入量、z₂は生産要素2の投入量、aとbは投入量の比率を決めるパラメーターである。このとき、生産要素の投入量は${\displaystyle {\frac {z_{1}}{a}}={\frac {z_{2}}{b}}}$を満たすように決まる。

レオンチェフ型生産関数は微分可能ではないため、要素投入量の比率と資源制約式から要素需要関数を求める。効用関数のときも同様、財の購入量比率と予算制約式から需要関数を求める。

例

1対1の完全補完

ゴムタイヤ（x₁）とスチールホイール（x₁）を生産要素としてタイヤ（T）という完成品を生産するとする。ゴムタイヤだけでは完成品はできず、スチールホイールだけでも完成しない。したがって、これら2つは互いに完全補完であると言える。このとき、タイヤを生産する生産関数は、

${\displaystyle T={\text{min}}\left\{x_{1},x_{2}\right\}}$

のように書ける。要素投入量は${\displaystyle x_{1}=x_{2}}$を満たすように決まる。

1対4の完全補完

タイヤ（T）と車体（X）を用いて自動車（Y）という完成品を生産するとする。車体1体につきタイヤが4つ必要なので、自動車を生産する生産関数は、

${\displaystyle Y={\text{min}}\left\{{\frac {T}{4}},X\right\}}$

のように書ける。要素投入量は${\displaystyle T=4X}$を満たすように決まる。車体が1体あるとき（${\displaystyle X=1}$）、タイヤが4つ必要である（${\displaystyle T=4\times 1=4}$）ことがわかる。タイヤが5つあっても車体が1体しかないのであれば、自動車は1台しか生産できないことは、

${\displaystyle Y={\text{min}}\left\{{\frac {5}{4}},1\right\}=1}$

であることからわかる。タイヤが5つと車体が2体あるときは、

${\displaystyle Y={\text{min}}\left\{{\frac {5}{4}},2\right\}={\frac {5}{4}}}$

となり、（自動車の台数が連続変数であることを許容するときは）自動車が5/4 = 1.25台生産されるという結果になる。

出典